Data Structure (8) - Graph
Definition
Graph
G = (V, E), where V is a set of vertices, and E is a set of edges.
For some reason unknown, people usually use n for the number of vertices, and m for the number of edges. |V|=n, |E|=m
An edge can not point to nowhere. It's always with 2 vertices.
- Complete Graph: A graph where all vertices are connected to each other.
- Connected Graph: A graph where all vertices are connected, not necessarily to each other.
- Acyclic Graph: A graph that has no cycles.
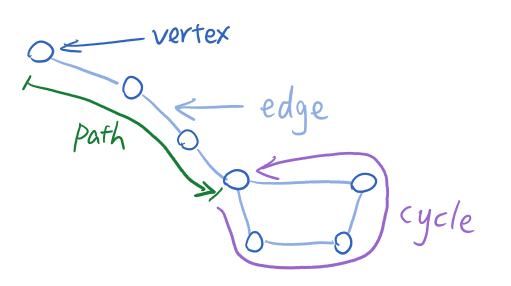
Incident Edges
I(v) = { {x,v} in E}
It's all the edges connected to the particular vertex.
Degree
D(v) = |I(v)|
The number of edges one vertex has.
Adjacent Vertices
A(v) = {x: {x, v} in E}
Path
Path(G1) = Sequence of vertices connected by edges.
Cycle
Cycle(G2) = Path with that goes in circle (with common begin and end vertex).
Simple Graph
A graph that has no self-loop or multi-edges.

Subgraph
G' = {V', E'} where V' belongs to V, and E' belongs to E and
if edge (u,v) belongs to E', then both u and v belongs to V'.
- Complete subgraph: A subgraph that is a complete graph
- Connected subgraph: All vertices in the subgraph are connected.
- Acyclic subgraph: A subgraph that has no cycle.
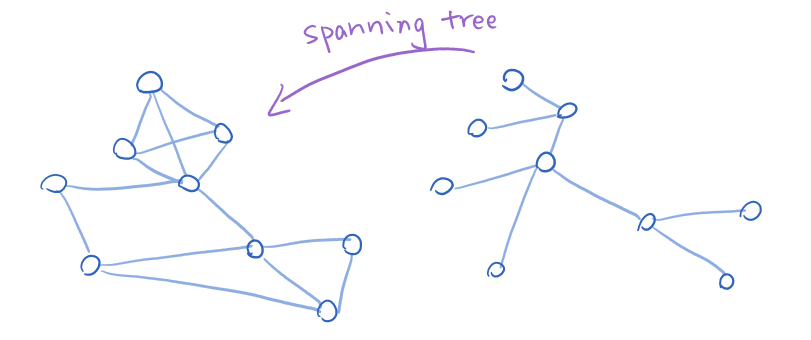
- Spanning Tree: A subgraph of graph G that contains all vertices of G with no cycle.
Observations / Calculations
In a graph with n vertices and m edges:
Minimum Edges:
- In a not-connected graph — 0
- In a connected graph — n-1
Maximum Edges:
- In a simple graph — n* (n-1) / 2
- In a not-simple graph — Infinity
Sum of degree(v) for all v in V = 2*m — or 2*|E|
Acyclic graph with n vertices has (n-1) edges.
Complete graph with n vertices has n* (n-1) / 2 edges.
Graph ADT
Data
- Vertices
- Edges
- Some data structure maintaining structure between vertices and edges
Functions
- insertVertex(K key) — key as label of vertex
- insertEdge(Vertex v1, Vertex v2, K key) — key as label of edge
- removeVertex(K key) or removeVertex(Vertex v)
- removeEdge(K key) or removeEdge(Vertex v1, Vertex v2)
- incidentEdges(Vertex v)
- areAdjacent(Vertex v1, Vertex v2)
-- to be continued
Ref:
