Disjoint Sets

Disjoint Sets is the data structure that supports the operation of adding one element (as their own set), [finding the label/canonical_name of one element in a set], and union 2 sets.

It can represents data like:

• Set1 (people whose favorite color's green)
• Set2 (people whose favorite color's blue)
• Set3 (people whose favorite color's red)
• ...

For set S = {S₁, S₂, S₃, ... , S_k}:

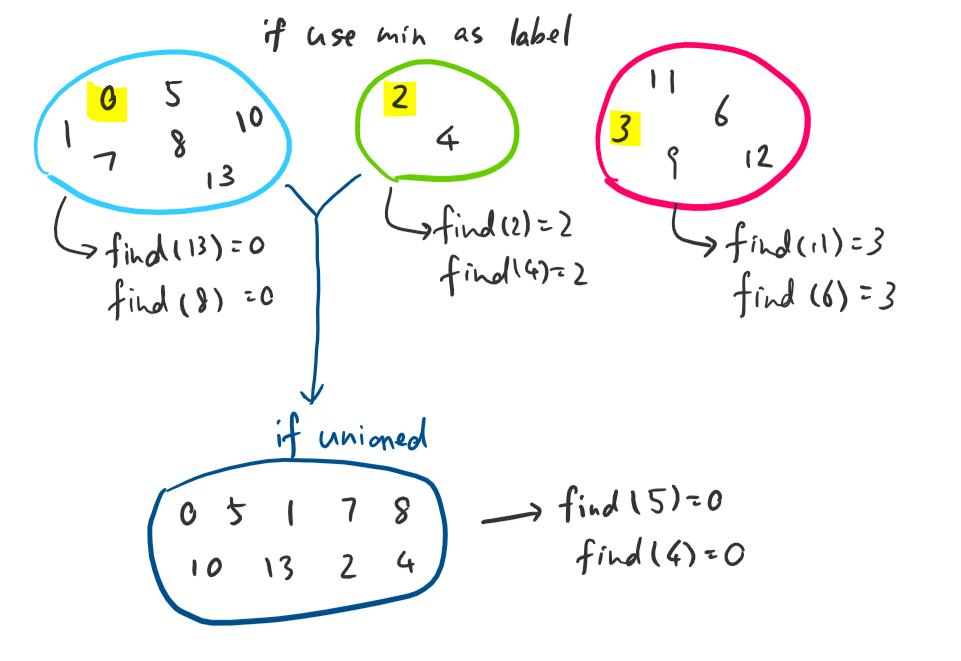
• find(S_i) where 1<=i<=k, gives representative integer of the set.

e.g. find(S_i) = min(S)

• join(Set1, Set2): join 2 sets into one. After this operation, find(S_i) where S_i was in Set1, will equal to find(S_j) where S_j was in Set2.

Key Ideas

• Each element exists in exactly one set.
• (Elements in sets are not ordered.)
• (If the element is not integer, hash it to integer first.)
• Every set is an equitant representation: 4 belongs to [0]_R, 8 belongs to [0]_R, then find(4)==find(8) is true (find(4) is 0, and find(8) is 0).

Build

When building disjoint sets:

• Start with everything separated
• Build sets by union the elements

Implementations

Array

Store label of item at array[hash(item)]

• find: O(1)
• union: O(n) – need to go through the array to update labels of one set

Up-Tree

Continue using an array where index is the key. Start all content in array as -1.

The value of array is:

• -1 if we've found the representative element
• The index of parent, if we haven't found the rep.

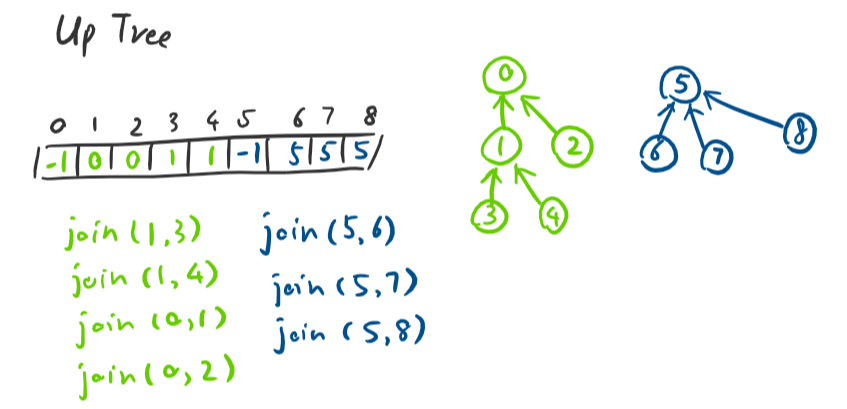
• find: O(h) where h is the height of the up-tree, and h is only bounded by n (size of the array). So we would like to keep the trees short.
• union: O(1)

Make up-trees faster: instead of storing -1 at roots, store -[number of nodes in tree] and use smart union:

int DisjointSets::find(int i) {
    if(arr_[i]<0) return i; // this is the root
    else return find(arr_[i]);
}

void DisjointSets::union(int r1, int r2) {
    arr_[r1] = r2; // points r1 to r2
}

void DisjointSets::unionBySize(int r1, int r2) {
    // union by size: keeps the number of nodes in a tree smaller
    
    int newSize = arr_[r1] + arr_[r2];
    
    if(arr_[r1]<arr_[r2]) { // r1 has more nodes
        arr_[r2] = r1; // so only -arr_[r2] nodes gets 1 layer higher
        arr_[r1] = newSize;
    } else {
        arr_[r1] = r2;
        arr_[r2] = newSize;
    }
}

void DisjointSets::unionByHeight(int r1, int r2) {
    // union by height: keeps the height of all trees smaller
    
    if(arr_[r1]< arr_[r2]) { // r1 is heigher
        arr_[r2] = r1; // so r1 doesn't get heigher
    } else if (arr_[r1]>arr_[r2]) {
        arr_[r1] = r2;
    } else { // tree gets higher no matter what
        arr_[r1] = r2;
        arr_[r2] -= 1;
    }
}

which makes the height of the trees: O(log(n))

Path Compression

int DisjointSets::find(int i) {
    if(arr_[i]<0) return i; // this is the root
    else {
        int root = find(arr_[i]);
        arr_[i] = root;
        return root;
    }
}

which makes find O(log(n)) amortized.

If we use both smart union and path compression?

The iterated log function:

log*(n) = {

0 , n<=1

1+log*(log(n)) , n>1

}

e.g. What's lg*(2⁶⁵⁵³⁵)?

1: lg(2⁶⁵⁵³⁵) = 65535,

2: lg(65535) = 16,

3: lg(16) = 4,

4: lg(4) = 2,

5: lg(2) = 1

so lg*(2⁶⁵⁵³⁵) = 5

union_find: O(m*α(n)) or O(α(n)) amortized, where n is number of items in Disjoint Sets. For all practice inputs, it's roughly O(1)

Ref:

• https://courses.engr.illinois.edu/cs225/fa2020/
• https://www.bilibili.com/video/BV1454y127Lk?p=29