Hash Table

A hash table has:

• A hash function h(k)
• An array
• Something that handles collisions and else

Dictionary in Python is a hash table.

Hash Function

A function that maps keys from key-space to an integer bounded by array size.

A hash function consists of 2 parts:

1. Takes key and produce some integer
2. A compression: shrinks large integer into range of array  (almost always mod N)

Characteristics of a good hash function:

• O(1) computation time
• Deterministic (it is not random): for k₁ = k₂ , h(k₁) = h(k₂)
• Satisfy SUHA (Simple Uniform Hashing Assumption)

SUHA:

• Keys are distributed uniformly in array.
• For i ≠ j, P(h(i)=h(j)) = 1/N, where N is the size of array (choosing index for i like randomly choosing an index of the array).
• (Hash by mod is not SUHA)

Collision Handling

Separate Chaining (open hashing)

Store linked lists (a pointer) in array.

For example: |S|=n, |Array| = N

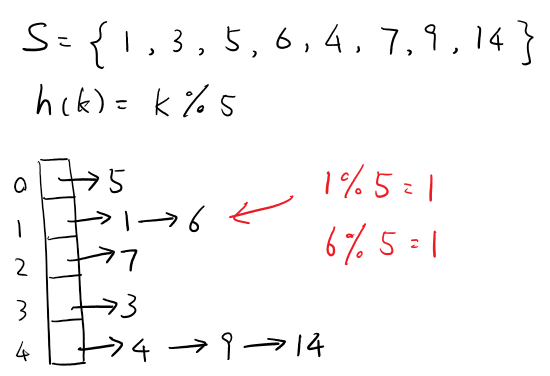
When collide, create a new node in the list in array[h(key)].

When hashing by mod:

• Insert: O(1)
• Find/Remove: O(n)  (Find/Remove: worst case collision)

When hashing satisfy SUHA:

• insert(O1)
• Find/Remove: O(n/N).

n/N is called load factor, it describes how efficiently the array is used.

Probe-based Hashing (closed hashing)

Use linear probing: when collide, just put into the next available space.

To make every key into array, size of array size should be no smaller than size of key space.

When find, calculate h(key) and try the value at that index. If it is not equal to key, find next, loop until finding the key in the array.

When hashing by mode:

• Insert: O(n)
• Find/Remove: O(n)

When SUHA:

• Insert: O(n/N)
• Find/Remove: O(n/N)

(Basically, no one uses this...)

Double Hashing (closed hashing)

If hashing once, collide, hash again, until finding available space.

• S = {k₁, k₂, ... , k_n},  |S| = n
• |Array| = N
• h₁(k) = k % N
• h₂ = 5 - (k%5)
• h(k,i) = (h₁(k) + i*h₂(k))%N, where i is the number of tries before finding available space
• N and all h₂ values should share no factors. Thus, we'd like N to be a prime

Comparisons

The expected number of probes for find(key) under SUHA,

where |Key Space| = n, |Array| = N,  

and a is load factor: (n/N)

Linear Probing:

• Successful: (1+1/(1-a))/2
• Unsuccessful: (1+1/(1-a))²/2

Double Hashing:

• Successful: 1/a * ln(1/(1-a))
• Unsuccessful: 1/(1-a)

Separate Chaining:

• Successful: 1+a/2
• Unsuccessful: 1+a

When heavily loaded, avoid linear probing and double hashing. When hash is SUHA and load factor is less than 0.75 (75% of the array space used), then linear probing and double hashing are pretty fast (double hashing is still generally faster than linear probing when a is under 0.75). When light loaded, these 2 can be faster than separate chaining.

When hash function is bad (not SUHA), usually separate chaining is better.

ReHashing

When having too many keys, and the array is filled (n/N>some constant value), we could expand array length to 2*N or next prime.

When changing N, as hash function is updated, we need to calculate new indexes for old keys in the new (expanded) array. This is called rehashing.

Rehashing takes O(n), but the chances we need to rehash is O(1) amortized, expected, given SUHA hashing.

Summary

Better Collision Strategy

Big records: separate chaining

Structure speed: double hashing

Constraints exist on hashing but not BSTs

• Amortized
• Probalistic runtime
• SUHA

Hash table only support exact matches, while BST supports range find.

In C++, map is implemented with red-black tree (it supports range find), and unordered_map is implemented with hashing.

Ref:

• https://courses.engr.illinois.edu/cs225/fa2020/
• https://www.bilibili.com/video/BV1454y127Lk?p=26