Kd-Tree

Short for k-dimension-tree. When search is not enough in one dimension, Kd-Trees may be used.

e.g. Search in 2D. Given x₁, x₂, y₁, y₂, find all points within the range.

If we don't want to go through all of the points – O(n) time

then, we could have a tree, where each root for sub-tree splits points in one axis.

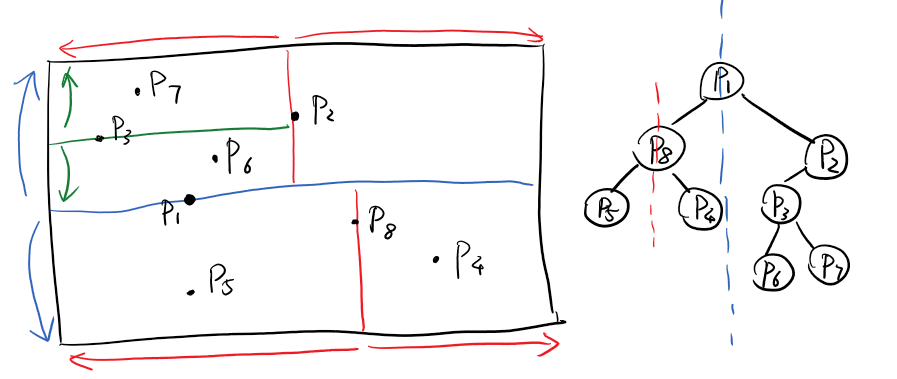
For the same sets of points, there are multiple ways to build a Kd-Tree.

For the example above, P₁ splits y-axis. All nodes in sub-tree on left are with Y less than Y_P1 , and all nodes in sub-tree on right are with Y larger than Y_P1 .

B-Tree

Motivation

When data set is huge, we can't always expect that we could fill all of them in main memory. They could be stored in disks, cloud, pingfs, etc.

If we have large seek time for data (e.g. all nodes are on different servers so the time going from one node to another is significant), then we would want to minimize the number of reads. In order to do that:

• Tree must be short
• Find relevant data
• Work local to a node is fast –> Do more things in a single node and decide where to go next. Have more children and larger nodes.

Definition

A B-Tree of order m:

• Is an m-way tree
• Will have (m-1) or less keys and 0~m children per node
• All keys within a node are ordered (sorted array)
• All leaves hold no more than (m-1) keys
• All internal nodes have exactly one more child than keys
• Root node can be a leaf or have [2,m] children
• All non-root, internal nodes have [ceil(m/2),m] children
• All leaves are on the same level
• Height is O(log_m(n)) – meaning the number of seeks will be O(log_m(n))

Build a tree that uses [1 network packet (TCP 1500 bytes)] / [1 disk block (512/8192 bytes)] per node.

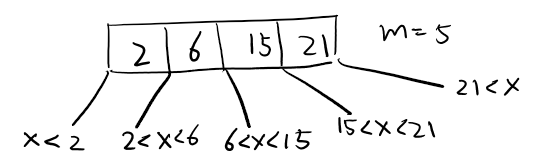
Example of B-Tree operations: https://www.cs.usfca.edu/~galles/visualization/BTree.html

B-Tree Insertion

When a B-Tree node reaches m keys:

Take the key in middle, push it up. Create 2 new nodes from the rest of this node and link to the one we just pushed up. Then insert.

B-Trees are built bottom up. When reaching m keys, they push nodes up.

Leaves of B-Tree are all at the same level.

B-Trees are perfect trees (perfect tree: all leaves have the same distance to root).

Leaves in B-Tree has at least ceil(m/2)-1 keys.

B-Tree Search

bool BTree::_exists(BTree &node, const K &key) {
    unsigned i;
    for( i=0; i<node.keys_ct_ && key<node.keys_[i]; i++) {
        // i < number of keys in node
        // find the first i, where key >= node.keys[i]
    }
    
    if(i<node.keys_ct && key == node.keys_[i]) {
        // if i is not out of the array, check if we've found the key
    	return true;
    }
    
    if(node.isLeaf()) { // base of recursion
        // if this is a leaf, and key is not here
        return false;
    } else {
        BTreeNode nextChild = node._fetchChild(i);
        // child could be in cloud -- anyway, handle it with the func
        return _exists(nextChild, key);
    }
    
}

ref: https://courses.engr.illinois.edu/cs225/fa2020/

ref: https://www.bilibili.com/video/BV1454y127Lk