Data Structure (3) - BST & AVL Tree
Binary Search Tree
A BST (binary search tree) is a tree T such:
- T = {} or
- T = {r, TL, TR} where all nodes in TL has keys less than r, all nodes in TR has keys greater than r, and TL and TR are BSTs.
// BST.h
#pragma once
template <typename K, typename V>
class BST {
public:
BST();
void insert(const K & key, const V & value);
void remove(const K & key);
K find(const K & key) const;
private:
struct TreeNode {
TreeNode *left, * right;
K key;
V value;
TreeNode(const K & k, const V & v): key(k), value(v), left(NULL), right(NULL){}
}
TreeNode *root_;
}
// cpp
template <typename K, typename V>
V BST::find(const K & key) {
TreeNode * node = _find(root_,key);
if(node) {
return node->value;
} else {
// deal with null case
return V();
}
}
template <typename K, typename V>
TreeNode *& _find(TreeNode *&node, const K & key) {
// returns a pointer reference of a treenode
// so if we want to find then update/insert, we can do it
if(node == nullptr) { return node;} // can't find the key
if(node->k==key) { // find exactly the key
return root;
} else {
if(node->k > key) {
return _find(node->left, key);
} else {
return _find(node->right, key);
}
}
}
template <typename K, typename V>
void BST::insert(const K & key, const V & value) {
_insert(root_, key, value);
}
template <typename K, typename V>
_insert(TreeNode *& root, const K & key, const V & value) {
TreeNode *& loc = _find(root,key);
if(loc == nullptr) {
loc = new TreeNode(key, value);
}
}
BST Remove:
IOP (In-order predecessor): left tree right most child. Largest node that is less than root.
IOS (In-order successor): right tree left most child. Smallest node that is larger than node.
When removing a node in BST:
- find the key
- find IOP or IOS
- swap node with key and IOP/IOS
- delete the node with key (it's 0-child delete now)
BST Worst Cases:
- find: O(h)
- insert: O(h)
- remove: O(h) —> O(h)+O(h) (find the node to remove, and find it's IOP/IOS)
- traversal: O(n)
For all BST, Lower bound: O(lg(n)) (when it is balanced), Upper bound: O(n) (when it is like a stick)
For all BST with n nodes (randomly sequenced), the average height of the trees is lg(n)
A balanced BST (O(h) for find, insert, delete, where h=lg(n), and O(n) for traverse) is a better choice for dictionary than sorted array (O(n) for insert, delete, traverse, O(lg(n) for find) and sorted list (O(n) for find, insert, delete, traverse).
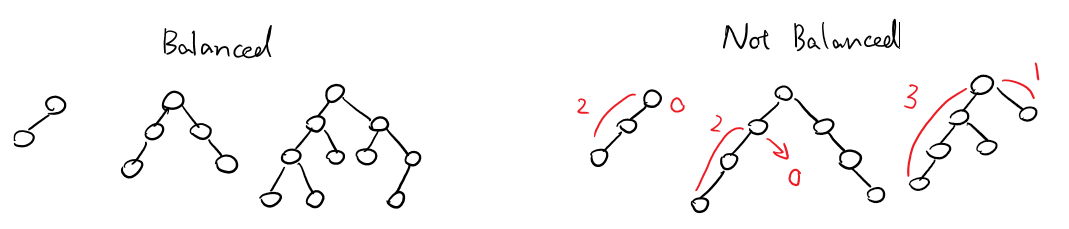
Height Balanced Tree
Height Balance: b = height(TR)-height(TL)
A tree T is height balanced if :
- T = {}
- T = {r, TL, TR}, |b|<=1, and TL and TR are balanced trees
A complete tree is always balanced.
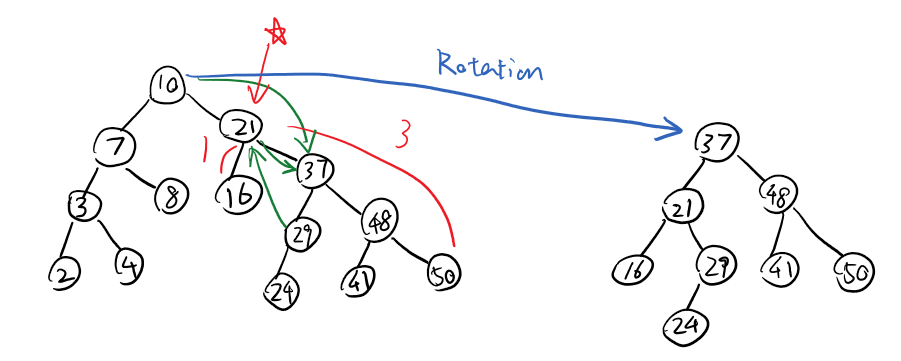
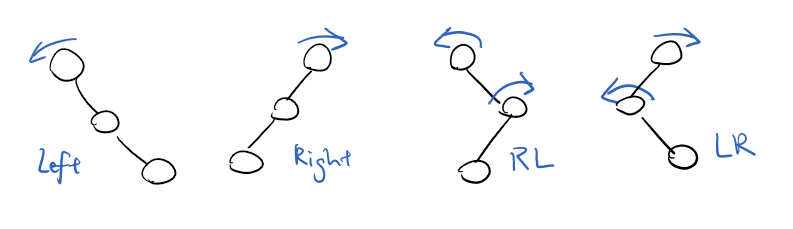
BST Rotation
- 4 kinds of rotations (L, R, LR, RL) (LR & RL for elbows)
- All rotations are local (subtrees are not impacted)
- All rotations are constant time: O(1)
- BST property maintained
Goal: produce trees of height h=O(log(n)) using only O(log(n)) time for each operation.
We call these trees AVL (Adelson-Velokii-Landis) trees.
AVL Tree
Three issues for consideration:
- Rotations: to fix imbalance
- Maintaining height: track height of each node
- Detect imbalance: when a node become out of balance
When a new node is inserted, only when the tree becomes taller, it becomes imbalanced.
Insert into an AVL tree:
- Insert at proper place – O(h)
- Check for imbalance – O(1)
- Rotate if necessary – O(1)
- Update height
struct TreeNode {
T key;
unsigned height;
TreeNode *left;
TreeNode *right;
}
template <class T>
void AVLTree::_insert(const T &x, TreeNode<T> *& t) {
if(t==NULL) { // base case. insert into empty tree
t = new TreeNode(x,0,NULL,NULL);
}
else if(x < t->key) { // insert into left sub-tree
_insert(x, t->left);
int balance = height(t->right) - height(t->left);
// helper func to handle when t doesn't have a left or right child
int leftBalance = height(t->left->right) - height(t->left->left);
if(balance == 2) { // out of balance
if(leftBalance == -1) { // a stick
rotateR(t);
}
else { // elbow
rotateLR(t);
}
}
}
else if(x > t->key) { // insert into right sub-tree
_insert(x, t->right);
int balance = height(t->right) - height(t->left);
int rightBalance = height(t->right->right) - height(t->right->left);
if(balance == 2) { // out of balance
if(rightBalance == 1) { // a stick
rotateL(t);
} else { // elbow
rotateRL(t)l
}
}
}
t->height = 1 + max(height(t->left), height(t->right));
}Analysis
Find runs at O(h)
Insert runs at O(h) find + O(1) add + O(1) rebalance, total O(h)
Remove runs at O(h) find + O(h) find IOP/IOS + O(1) remove + h*O(1) rebalance, total O(h)
Where h is O(log(n)).
Minimum number of nodes
Let N(h) be smallest number of nodes in an AVL tree of height h:
N(-1) = 0,
N(0) = 1,
N(1) = 2,
...
N(h) = 1 + N(h-1) + N(h-2),
which is, root + a sub tree of (h-1) and a sub tree of (h-2), balance = 1 or -1
So, N(h) > N(h-1) + N(h-2) >= 2*N(h-2) >= 2h/2 (when h>=1)
An AVL tree of height h has at least 2h/2 nodes.
Invert it:
n >= N(h) > 2h/2,
n>= 2h/2
log(n) >= h/2
h<= 2 log(n) — where log(n) > 0
So for an AVL tree, h=O(log(n))
Summary of Balanced BST Trees
AVL
- Max height: 1.44 * lg(n)
- Rotations:
- find – 0 rotation
- insert – 1 rotation at most (LR, RL count as 1)
- remove – h rotations at most, where h is O(log(n))
Red-Black Tree
- Max height: 2 * lg(n)
- Constant numbers of rotations:
- insert – 2 rotations at most
- remove – 3 rotations at most
- Works better with modern hardware (more caches and predicters)
- (C++'s standard map is Red-Black tree)
// map API
map<string,int> grades;
//....
grades["someone"] = 100;
cout << "Someone's grade is: " << grades["someone"] << endl;
grades.erase("someone");
Pros of Cons of BST
Pros
Running time O(log(n)), improvement over lists and arrays as dictionary.
Good for:
- Approximate find: Each step (the sub-tree) is closer to target
- Range and nearest neighbor find
Cons
- Never O(1)
- In-memory requirement: following pointer is O(1) and fast -> assume everything is in memory (if it points to resources elsewhere, like on another computer or database over Internet, it could be slow)
ref: https://courses.engr.illinois.edu/cs225/fa2020/
