Tree

A tree is an acyclic graph ( a graph that has no circle in it)

Tree ADT

ADT: Abstract Data Type

• insert: add data (node) to tree
• remove: remove data (node) from tree
• create: create empty tree
• traversal: iterate over data

// BinaryTree.h
#pragma once

template <typename T>
class BinaryTree {
    public:
    /*....*/
    private:
        struct TreeNode {
            T data_;
            TreeNode * left;
            TreeNode * right;
        }
        
        TreeNode * root_;
}

Binary Tree

A binary tree is either:

• T = {root, T_L, T_R}    A root, plus a left tree, plus a right tree. Or
• An empty set (empty tree / tree with no node)

Tree Property: Height

Definition

Length of the longest path from the root to a leaf.

Note

• Count only the path (arrows), not the nodes.
• If the tree has k layers, it's height h = k-1.
• The height of an empty tree is -1.
• The height of a tree with only one node is 0.

Calculation

height(T) = max(height(T_L), height(T_R)) + 1

Maximum number of nodes a binary tree of height h can have:

m(h) = 2^(h+1)-1

Minimum height of a tree with n nodes: log(n)

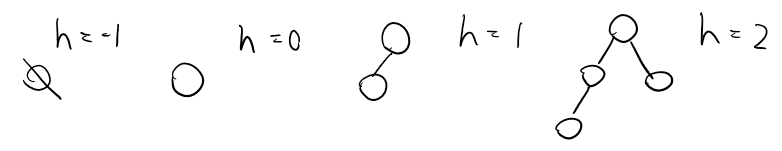
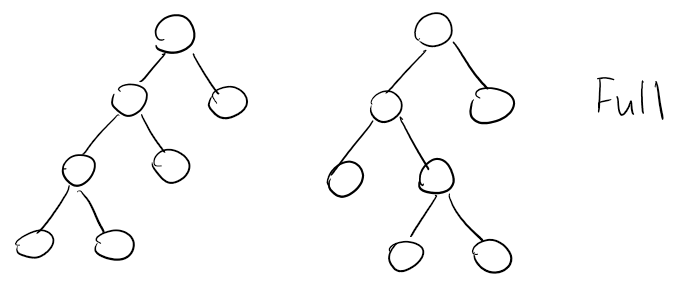
Tree Property: Full

A tree is full if and only if:

• The tree is empty
• F = {root, T_L, T_R} where T_L and T_R are both empty
• or T_L and T_R are both not empty

In simple terms, each node has 0 or 2 children.

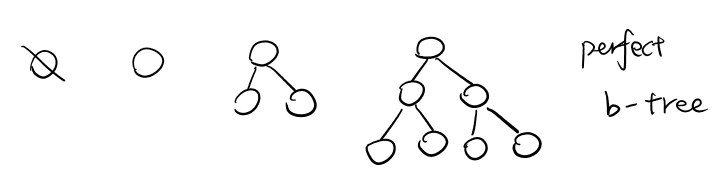
Tree Property: Perfect

Let P(h) be a perfect tree of height h, then:

• P(-1) is an empty tree
• P(h) = {r, T_L, T_R} where T_L and T_R are P(h-1)

All perfect trees are full and complete, but not all full trees are perfect.

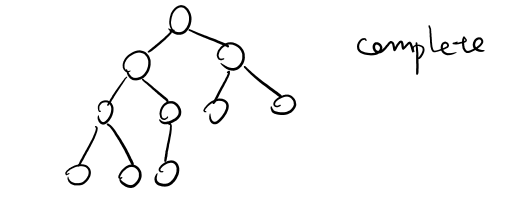
Tree Property: Complete

Definition

A perfect tree for every level except the last, where the last level if "pushed to the left".

For all levels k in [0, h-1], k has 2^k nodes. For level h, all nodes are "pushed to the left"

A complete tree C of height h, C(h):

• C(-1) is an empty tree
• When h>=0, C(h) = {r, T_L, T_R} and either:
• TL is C(h-1) and TR is P(h-2) — when left is not filled, right can't have last layer of leaves, but right must be a (h-2) perfect tree
• or
• TL is P(h-1) and TR is C(h-1) — when left is filled, right can fill up to h-1

How many null pointers does a binary tree of n nodes has?

Theorem: If there are n data items in a binary tree, then there are n+1 NULL pointers.

Base Cases:

• NULLs(0) = 1 — In a tree of 1 node, there is 1 pointer, root, which is null.
• NULLs(1) = 2
• NULLs(2) = 3

Induction Hypothesis:

Suppose NULLs(n) = n+1  for 0<=n<=k

Consider an arbitrary tree T containing k nodes:

T = {r, T_L, T_R}    (split the tree into root, left tree, right tree)

if T_L has q nodes, then T_R has k-q-1 nodes.

then NULLs(k) = NULLs(q) + NULLs(k-q-1)

by hypothesis,

NULLs(k) = NULLs(q) + NULLs(k-q-1) = (q+1) + (k-q-1+1) = k+1

Traversal

Traversal vs Search:

Traversal: visits every node in the tree exactly once.

Search: finds one element in the tree.

Recursive:

template <class T>
void BinaryTree<T>::PreOrder(TreeNode * cur) {
    if(cur) { // checking if the node is empty
        cout << cur->data << endl; // access root data
        
        PreOrder(cur->left); // go left
        PreOrder(cur->right); // go right
    }
    
    return;
}


template <class T>
void BinaryTree<T>::InOrder(TreeNode * cur) {
    if(cur != NULL) {
        InOrder(cur->left); // go left
        
        cout << cur->data << endl; // access root data
        
        InOrder(cur->right); // go right
    }
    
    return;
}
// standard infix notation in computation
// e.g. (1-(a/b))*(2+3)
// operation on root, and figures/operations on leaves


template <class T>
void BinaryTree<T>::PostOrder(TreeNode * cur) {
    if(cur!=NULL) {
        PostOrder(cur->left);
        PostOrder(cur->right);
        cout << cur->data << endl;
    }
    
    return;
}
// RPN (Reverse Polish Notation) in computation
// or stack order
// e.g. 3 4 5 * -
// that's 3-4*5

Non-recursive (level order):

• Go layer by layer
• BFS (Breadth first search)
• O(n) runtime

Steps:

1. Create an empty queue and enqueue root.
2. Pop queue and process where process is:
3. Access data, then enqueue all child nodes.
4. Repeat step 2 until queue is empty.

Depth First Search

Post/Pre/In order.

Good at finding data at the leaves. If lucky, very fast.

Most memory needed: O(h)  (your stack will never gets over the height of the tree)

Breadth First Search

Level order.

Good at finding data near the root.

Most memory needed: O(2^h) or O(n) (leave nodes in queue)

If key is in tree, it will find it even if the tree is infinite.

ref: https://courses.engr.illinois.edu/cs225/fa2020/